Badewanne. Warum das Material bei der Badewanne so wichtig ist Wenn ich an meine erste Badewanne zurückdenke, fällt mir sofort das Material […]
SanctuaryVF™
Tapete
Tapete. Warum die richtige Vorbereitung bei der Tapete so wichtig ist Wenn ich zurückdenke an meine ersten Tapezier-Versuche, merke ich erst, wie […]
Gartendusche
Gartendusche. Warum eine Gartendusche im Sommer unverzichtbar ist Im Sommer gibt es kaum etwas Erfrischenderes als eine schnelle Abkühlung im eigenen Garten. […]
Barhocker
Barhocker. Warum die richtige Sitzhöhe bei Barhockern so wichtig ist Als ich das erste Mal Barhocker für meine Küche ausgesucht habe, dachte […]
Vordach
Vordach. Warum ein Vordach mehr als nur Schutz vor Regen ist Ich erinnere mich noch gut, wie ich das erste Mal ein […]
Sanremo
Sanremo. und seine bezaubernde Blumenpracht Sanremo ist berühmt als die „Stadt der Blumen“. Wenn man durch die Straßen schlendert, begegnet man überall […]
Balkonset
Balkonset. Warum die Wahl des richtigen Balkonsets so wichtig ist Ich sag’s dir, Balkonset kaufen ist nicht einfach nur “Tisch und Stühle […]
Fototapete Fridge
Fototapete Fridge. Warum eine Fototapete auf den Kühlschrank eine coole Idee ist Ehrlich gesagt, war ich anfangs ziemlich skeptisch, ob so eine […]
Gartenzaun Holz
Gartenzaun Holz. Warum ein Holz-Gartenzaun die beste Wahl für deinen Garten ist Holz als Material für den Gartenzaun hat für mich immer […]
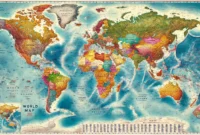
Landkarte Weltkarte Länder
Landkarte Weltkarte Länder. Warum Landkarten im Blog mehr bringen als nur hübsche Bilder Wenn du mich fragst, Landkarten sind so viel mehr […]